LUNES 4 DE MAYO
Ecuaciones de Cauchy-Riemann
Las ecuaciones de Cauchy-Riemann son dos ecuaciones diferenciales parciales que son básicas en el análisis de funciones complejas de variable compleja, debido a que su verificación constituye una condición necesaria (aunque no suficiente) para la derivabilidad de este tipo de funciones.
Sea una función compleja  , con
, con 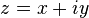 . Se sabe que
. Se sabe que  se puede descomponer en suma de dos funciones reales de dos variables
se puede descomponer en suma de dos funciones reales de dos variables  y
y  , de manera que
, de manera que  . Si la función
. Si la función  es derivable en un punto
es derivable en un punto 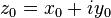 entonces deben verificarse las condiciones de Cauchy-Riemann:
entonces deben verificarse las condiciones de Cauchy-Riemann:
 , con
, con 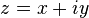 . Se sabe que
. Se sabe que  se puede descomponer en suma de dos funciones reales de dos variables
se puede descomponer en suma de dos funciones reales de dos variables  y
y  , de manera que
, de manera que  . Si la función
. Si la función  es derivable en un punto
es derivable en un punto 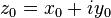 entonces deben verificarse las condiciones de Cauchy-Riemann:
entonces deben verificarse las condiciones de Cauchy-Riemann:

donde
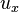 significa la derivada parcial de la función
significa la derivada parcial de la función  respecto a la variable
respecto a la variable  , usualmente simbolizado
, usualmente simbolizado  . Análogamente para
. Análogamente para  ,
,  y
y  .
.
Además se cumple que el valor de la derivada en el punto, de existir, debe ser:

FUNCIONES ANALÍTICAS
f(Z), función compleja se dice que es funcion analítica en Zo ssi , f(Z) es derivable para todo Z en algun disco abierto D de centro Zo, de forma concreta D: |Z-Zo| < r
FUNCIONES ARMÓNICAS
Sea f(z) una función analítica que satisface las ECR
Entonces si se cumple que :
d^2u + d^2u = 0 ^ d^2v + d^2v = 0
dx^2 dy^2 dx^2 dy^2
Se dice que : u(x,y) ^v(x,y) son funciones armónicas
∇^2u = d^2u + d^2u = 0
dx^2 dy^2 Ecuaciones de laplace
∇ ^2v = d^2v + d^2v = 0
dx^2 dy^2
- u(x,y) ^ v(x,y) se dice que son funciones conjugadas armónicas una de la otra.
- Toda función f(z)=u(x,y) + iv(x,y) que satisface las ecuaciones de laplace se llaman funciones armónicas.
- Se pueden denotar también :
uxx+uyy=0
vxx+vyy=0 - En física se conocen como ecuaciones de potencial.
EJEMPLO:

JUEVES 14 Y JUEVES 21


EJEMPLO:

TEOREMA INTEGRAL DE CAUCHY
Si f(z) es analítica en un dominio simplemente conexo D y su derivada es continua en D entonces para cualquier contorno cerrado simple contenido en D se tiene:
FÓRMULA INTEGRAL DE CAUCHY
Enunciado 1
Sea f(z) una función analítica en un dominio simplemente conexo D. Entonces para cualquier punto 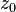 contenido en el interior de D y para cualquier camino C cerrado simple también contenido en el interior de D que contenga al punto se tiene
contenido en el interior de D y para cualquier camino C cerrado simple también contenido en el interior de D que contenga al punto se tiene
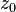 contenido en el interior de D y para cualquier camino C cerrado simple también contenido en el interior de D que contenga al punto se tiene
contenido en el interior de D y para cualquier camino C cerrado simple también contenido en el interior de D que contenga al punto se tiene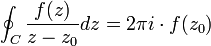
donde la integración está tomada en sentido antihorario.
Enunciado 2
Sea  una función analítica sobre
una función analítica sobre  ,
,  un camino (una curva diferenciable con continuidad a trozos) cerrado y
un camino (una curva diferenciable con continuidad a trozos) cerrado y 
 una función analítica sobre
una función analítica sobre  ,
,  un camino (una curva diferenciable con continuidad a trozos) cerrado y
un camino (una curva diferenciable con continuidad a trozos) cerrado y 

Siendo 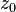 un punto que no esté sobre
un punto que no esté sobre  ,
,  el índice del punto respecto a la curva (el número de veces que la curva rodea al punto teniendo en cuenta el sentido con que lo hace).
el índice del punto respecto a la curva (el número de veces que la curva rodea al punto teniendo en cuenta el sentido con que lo hace).
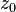 un punto que no esté sobre
un punto que no esté sobre  ,
,  el índice del punto respecto a la curva (el número de veces que la curva rodea al punto teniendo en cuenta el sentido con que lo hace).
el índice del punto respecto a la curva (el número de veces que la curva rodea al punto teniendo en cuenta el sentido con que lo hace).
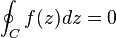
No hay comentarios:
Publicar un comentario