 27 de Abril
27 de Abril
La función exponencial
La Fórmula o relación de Euler, establece que:
para todo número real
x, que representa un ángulo en el plano complejo. Aquí,
e es la base del logaritmo natural,
i es launidad imaginaria,

y

son las funciones trigonométricas seno y coseno.
O bien se suele expresar como:
siendo

la variable compleja definida por
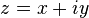
La fórmula de Euler también permite interpretar las funciones seno y coseno como meras variaciones de la función exponencial:
Estas fórmulas sirven asimismo para definir las funciones trigonométricas para argumentos complejos

. Las dos ecuaciones anteriores se obtienen simplemente resolviendo las fórmulas
para el seno y el coseno.
Logaritmos complejos
Para definir una fórmula para Log
z, se empieza con la representación de
z en forma polar,
z =
reiθ. Dado
z, la forma polar no es única debido a la posibilidad de sumar un múltiplo entero de 2
π a
θ, pero puede
hacerse única bajo el requisito de que
θ caiga en el intervalo (−
π,
π]; este
θ se denomina valor principal del argumento, y normalmente se escribe como
Arg z. Entonces, el valor principal del logaritmo puede escribirse como
Por ejemplo, Log(-3i) = ln 3 − πi/2.
23 de Abril
FUNCIONES COMPLEJAS
Recordemos que una función real de variable real sobre un conjunto de números reales es una función que asigna a un número real ∈D otro número real = f(x).
Este concepto se generaliza fácilmente al caso complejo:
Una función compleja de variable compleja definida sobre un conjunto de números complejos es una función que asigna a cada número complejo ∈D otro número complejo = f(z) y la representamos con la notación : D→ℂ.
El conjunto se llama, igual que en el caso de las funciones reales,dominio de . Igualmente, el conjunto de las imágenes de se llama imagen de
27 de Abril
Límites y Continuidad de una Función Compleja de Variable Compleja
Sea ƒ: D ⊆ C → C, una función compleja de variable compleja z, definida en la región D ⊆ C excepto posiblemente en Z0 entonces diremos que el límite de f(z) es el número complejo L cuando z se aproxima a Z0 , si y sólo sí, para todo ξ>0, existe un δ>0, tal que:
0< ||z- Z0||< δ, entonces ||f(z) –L||< ξ
Propiedades:
Se dice que lim (z)→(z0) f(z) = ∞ si para todo M > 0 existe δ > 0 tal que si |z − z0| < δ, entonces |f(z)| > M.
Se dice que lim (z)→∞ f(z) = l si para todo ε > 0 existe N > 0 tal que si |z| > N, entonces |f(z)−l| < ε.
Por último, diremos que lim (z)→∞ f(z) = ∞si para todo M > 0 existe N > 0 de manera que si |z| > N, entonces |f(z)| > M.
Los límites de funciones de variable compleja tienen las siguientes propiedades que son análogas a aquellas de los límites de funciones del plano.
(L1) Si el límite existe, entonces es único.
(L2) lim (z)→(z0)f(z) = l si y sólo si lim (z)→(z0) Ref(z) = Rel ylim (z)→(z0) Imf(z) = Iml.
Continuidad de una Función Compleja
Una vez estudiada la noción de límite de una función de variable compleja, pasamos a abordar la continuidad de las misma. Como en el caso real una función f : A ⊆ C → C se dirá continua en z0 ∈ A si existe el límite de f(z) cuando z→z0 y además lim (z)→(z0), f(z) = f(z0).
La función f se dirá continua en A si es continua en todo punto de A.
Como no podía ser de otra manera, la continuidad de f ocurre si y sólo si son continuas la funciones coordenadas Ref e Imf.
30 de Abril
Derivadas de Funciones Complejas
Aunque la definición es idéntica en su forma a la derivada real, pues f : A ⊆ C → C se dirá derivable en z0 ∈ Int(A) si existe y es finito el límite.

 .
. .
.





 (
(







 la variable compleja definida por
la variable compleja definida por 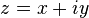
 . Las dos ecuaciones anteriores se obtienen simplemente resolviendo las fórmulas
. Las dos ecuaciones anteriores se obtienen simplemente resolviendo las fórmulas
No hay comentarios:
Publicar un comentario